Decision Linear assumption
The Decision Linear (DLIN) assumption is a mathematical assumption used in elliptic curve cryptography. In particular, the DLIN assumption is useful in settings where the decisional Diffie–Hellman assumption does not hold (as is often the case in pairing-based cryptography). The Decision Linear assumption was introduced by Boneh, Boyen, and Shacham [1].
Informally the DLIN assumption states that given 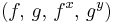 , with
, with 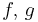 random group elements and
random group elements and 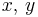 random exponents, it is hard to distinguish
random exponents, it is hard to distinguish 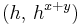 (for random
(for random  ) from
) from 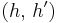 (for independently random
(for independently random 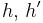 ).
).
References
- ^ Dan Boneh, Xavier Boyen, Hovav Shacham: Short Group Signatures. CRYPTO 2004: 41–55
|
|||||||||||||||||||||||||||||